FUNCION CUADRATICA

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:

f(x) = ax 2 + bx + c

donde a , b y c (llamados términos ) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero .

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

Así,

ax 2 es el término cuadrático

bx es el término lineal

c es el término independiente

Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es una ecuación completa , si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta .

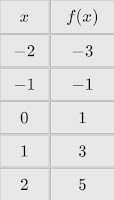
Podemos construir una parábola a partir de estos puntos:

*VERTICE

Por el vértice pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax 2 ) :

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x 2 − 3x − 5Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x 2 + 2x + 3

EJEMPLO

Representar la función f(x) = x² − 4x + 3.

Vértice

x_v = − (−4) / 2 = 2     y_v= 2² − 4· 2 + 3 = −1       

 V(2, −1)

Puntos de corte con el eje OX

x² − 4x + 3 = 0

        
(3, 0)      (1, 0)

Punto de corte con el eje OY

(0, 3)

FUNCIONES LINEALES

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación:

 f(x) = mx + b ó y = mx + b

llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

M ES LA PENDIENTE DE LA RECTA.

La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.

i m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.  

f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.

EJEMPLO

f (x) = 24x

m = la pendiente es 24

la recta no cruza el eje de las y

TIPOS DE FUNCIONES

FUNCIONES ALGEBRAICAS
Una función es algebraica si la variable independiente   x   solo tiene operaciones algebraicas: suma, resta, multiplicación, elevar a potencias y extraer raíces.
Las funciones algebraicas se clasifican en:
Funciones explicitas
Si se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x − 2

Funciones implicitas

Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x − y − 2 = 0

FUNCIONES POLINOMICAS

Son las funciones que vienen definidas por un polinomio. f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es  , es decir, cualquier número real tiene imagen.

FUNCIONES RACIONALES

El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

FUNCIONES RADICALES

El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

FUNCIONES TRASCENDENTES

La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

FUNCIONES EXPONENCIALES 

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

FUNCIONES LOGARITMICAS

La función logarítmica en base a es la función inversa de la exponencial en base a.

FUNCIONES TRIGONOMETRICAS

• Función seno f(x) = sen x

• Función coseno f(x) = cos x

• Función tangente f(x) = tg x

• Función cosecante f(x) = cosec x

• Función secante f(x) = sec x

• Función cotangente f(x) = cotg x

EJEMPLOS:

REPRESENTACION GRAFICA DE FUNCIONES

Supongamos que tenemos una función  f(x). Para representarla gráficamente debemos primero encontrar su dominio para saber en que puntos debemos evaluarla.
Una vez encontrado el dominio procederemos a hacer la representación. ¿Cómo lo haremos? Bien, la manera más simple y sencilla es mediante una tabla de valores, es decir, daremos valores a la variable (x) y encontraremos el valor de f(x) y dibujaremos el punto encontrado, (x,f(x)) en el plano usando las coordenadas cartesianas.

EJEMPLO
Tomemos la función  f(x) = 2x+1 y vamos a hacer la tabla de valores:  

y por lo tanto encontramos los pares de puntos:

los que dibujaremos en el plano XY  y los uniremos con una línea. Al final obtenemos: 

EJEMPLO

         

DEFINICION, DOMINIO, RANGO DE UNA VARIABLE REAL

Se llama función real de variable real a cualquier aplicación f:D→R con  R, es decir,a cualquier correspondencia que asocia a cada elemento de D un único número real.

Habitualmente, la notación que se usa para representar una función es  y = f (x), donde x es la variable independiente,y la variable dependiente y f la aplicación que indica como se obtiene el valor de y conocido el valor d x.

El dominio de una función está dado por el conjunto de valores que puede tomar una función. Por ejemplo si f(x) = x;  esta variable x puede tomar cualquier valor, no tiene ninguna restricción, entonces su dominio esta compuesto por todos los números Reales.

Como los valores de la función están dados para la variable independiente (x), los valores que puede tomar la función son aquellos para los cuales al evaluar la función para un valor de x, su resultado nos da un número Real.

Para buscar el dominio de la función, se debe analizar para qué valores de x la función produce como resultado un número Real.

En general se pueden seguir las siguientes recomendaciones para obtener el dominio de una función o de una expresión algebraica:

• No puede haber una raíz cuadrada ( ó cualquier raíz par ) negativa, pues se trataría de un número imaginario que no hace parte de los Reales.
• Un fraccionario no puede contener por denominador cero, pues la expresión queda indeterminada.                                                                                                           Dominio de la función polinómica entera                                          El dominio es R, cualquier número real tiene imagen.             Dominio de la función racional                                                        El dominio es R menos los valores que anulan al denominador (no puede existir un número cuyo denominador sea cero).
• Dominio de la función irracional de índice impar
  El dominio es R.
  Dominio de la función irracional de índice par
  El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
  Dominio de la función logarítmica
  El dominio está formado por todos los valores que hacen que el radicando sea mayor que cero.
  Dominio de la función exponencial
  El dominio es R.
  Dominio de la función seno
  El dominio es R.
  Dominio de la función coseno
  El dominio es R.
  
  
  
  

El rango de una función, está determinado por todos los valores que pueden resultar al evaluar una función. Son los valores obtenidos para la variable dependiente (y). También se puede expresar como todos los valores de salida de la función.

INECUACIONES

Una inecuación es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos:

<	menor que	2x − 1 < 7
≤	menor o igual que	2x − 1 ≤ 7
>	mayor que	2x − 1 > 7
≥	mayor o igual que	2x − 1 ≥ 7

La solución de una inecuación es el conjunto de valores de la variable que verifica la inecuacíón.
Podemos expresar la solución de la inecuación mediante:

1. Una representación gráfica.
2. Un intervalo.

EJEMPLO

2x − 1 < 7 =

           2x < 8     x < 4

                                                (-∞, 4)

2x − 1 ≤ 7=

         2x ≤ 8     x ≤ 4

                                               (-∞, 4]

Inecuaciones de primer grado con una incógnita.

Se resuelven por separado las inecuaciones y se toman como soluciones los intervalos comunes de las soluciones
5x + 6 < 3x - 8
3x > 2
La solución de la primera ecuación es:
5x - 3x < -8 - 6
2x < -14
x < -7
La solución de la segunda ecuación es:
3x > -2
x < -2/3
La solución del sistema sería x < -7.

Inecuaciones de segundo grado.

Se resuelve como una ecuación de segundo grado y se estudian los signos que obtenemos con las soluciones.
x2 - 5x + 6 > 0
Las soluciones de la ecuación x2 - 5x + 6 = 0 son x = 3 y x = 2. 

Por lo tanto x2 - 5x + 6 = (x - 2)(x - 3).

Tenemos que estudiar los signos cuando x toma valores desde menos infinito hasta 2, desde 2 hasta 3 y desde 3 hasta infinito .
x - 2 es negativo para los valores entre menos infinito y 2.
x - 2 es positivo para los valores entre 2 y 3.
x - 2 es positivo para los valores entre 3 e infinito.
x - 3 es negativo para los valores entre menos infinito y 2.
x - 3 es negativo para los valores entre 2 y 3.
x - 3 es positivo para los valores entre 3 e infinito.

Por lo tanto, multiplicando los signos en los mismos intervalos:

x2 -5x + 6 es positivo para los valores entre menos infinito y 2.
x2 - 5x + 6 es negativo para los valores entre 2 y 3.
x2 - 5x + 6 es positivo para los valores entre 3 e infinito.

Inecuaciones de grado superior a dos

Se descomponen en inecuaciones de grado uno y dos.

Inecuaciones fraccionarias

Son las inecuaciones en las que tenemos la incógnita en el denominador.
Se pasan todos los términos a un lado del signo de desigualdad y se reducen a común denominador.
Después se buscan las soluciones y estudiamos el signo (como en el caso de las ecuaciones de segundo grado). Hay que tener en cuenta que las soluciones que anulan el denominador no valen.

Inecuaciones con valor absoluto

Se resuelven convirtiendo la función valor absoluto en dos inecuaciones

|x - 3| > 3

conlleva que -3>(x-3)>3, luego

x-3 >3 

-3>x-3  

son los puntos mayores que 0 y menores que 6.

ECUACIONES

Una ecuación es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa generalmente por las últimas letras del abecedario: “x”, “y” o “z”, aunque puede utilizarse cualquiera otra letra. 

TIPOS
Las ecuaciones suelen clasificarse según el tipo de operaciones necesarias para definirlas y según el conjunto de números sobre el que se busca la solución. Entre los tipos más comunes están:
    ECUACIONES ALGEBRAICAS

• De primer grado o lineales
• De segundo grado o cuadráticas
• De tercer grado o cúbicas
• Diofánticas o diofantinas
• Racionales, aquellas en las que uno o ambos miembros se expresan como un cociente de polinomios

    ECUACIONES TRASCENDENTES

Es cuando involucran funciones no polinómicas, como las funciones trigonométricas, exponenciales, logarítmicas, etc.

    

    ECUACIONES DIFERENCIALES

• Ordinarias
• En derivadas parciales

    ECUACIONES INTEGRALES

    ECUACIONES FUNCIONALES

Una ecuación funcional es aquella en la que algunas de las constantes y variables que intervienen no son realmente números sino funciones; y si en la ecuación aparece algún operador diferencial se llama ecuación diferencial.

    ECUACIONES LINEALES 

Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).

Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1. Se reducen los términos semejantes, cuando es posible.
2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.
3. Se reducen términos semejantes, hasta donde es posible.

4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.

EJEMPLO

ECUACION CUADRATICA

Una ecuación de segundo grado es toda expresión de la forma: 

ax² + bx +c = 0 con a ≠ 0.

EJEMPLO

ECUACION CUBICA 

Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica:

donde a, b, c y d (a ≠ 0) son números que pertenecen a un cuerpo, usualmente a R o a C. 

Una ecuación cualquiera de tercer grado, una vez simplificada y ordenada convenientemente, se podrá escribir como: ax3 + bx2 + cx + d = 0 En general puede tener entre una y tres soluciones, según los factores en que se pueda descomponer el polinomio correspondiente al primer miembro.

EJEMPLO

ECUACION CUARTICA

Una ecuación de cuarto grado o ecuación cuártica con una incógnita es una ecuación algebraica que se puede poner bajo la forma canónica: 

donde a, b, c, d y e (siendo a ≠0) son números que pertenecen a un cuerpo, usualmente a los reales R o loa complejos C.

EJEMPLO